Abstract
Quantum tunneling can dominate torsional isomerization in light-atom systems. This ACS-style note demonstrates an end-to-end workflow in the improved_tunnel codebase using hydrogen peroxide as a model system. The workflow couples a relaxed dihedral scan with semiclassical tunneling corrections (WKB, SCT, and Eckart) and prepares a ring-polymer instanton input for i-PI. The calculations shown here use the package’s mock quantum chemistry engine to generate illustrative data; the goal is reproducible method documentation and visualization, not benchmark energetics.
Introduction
Tunneling remains a central motif in chemical kinetics, especially for light atoms and torsional rearrangements. Semiclassical approaches such as WKB and small-curvature tunneling approximate barrier transmission while preserving practical computational cost.[2] Analytical barriers (e.g., Eckart) provide a compact reference model for transmission functions.[1] For deep tunneling, path-integral approaches such as ring-polymer instantons provide a more rigorous treatment of quantum delocalization.[3] This post links these pieces into a single workflow and documents how to run it, plot results, and hand off an instanton path to i-PI.[4]
Experimental Section
Workflow overview
The calculations use the improved_tunnel workflow runner. A relaxed scan is carried out over the H-O-O-H dihedral, followed by tunneling corrections and Arrhenius-rate postprocessing. The results are then summarized with plots and tables, and an i-PI XML input is generated for instanton optimization.
Potential energy scan
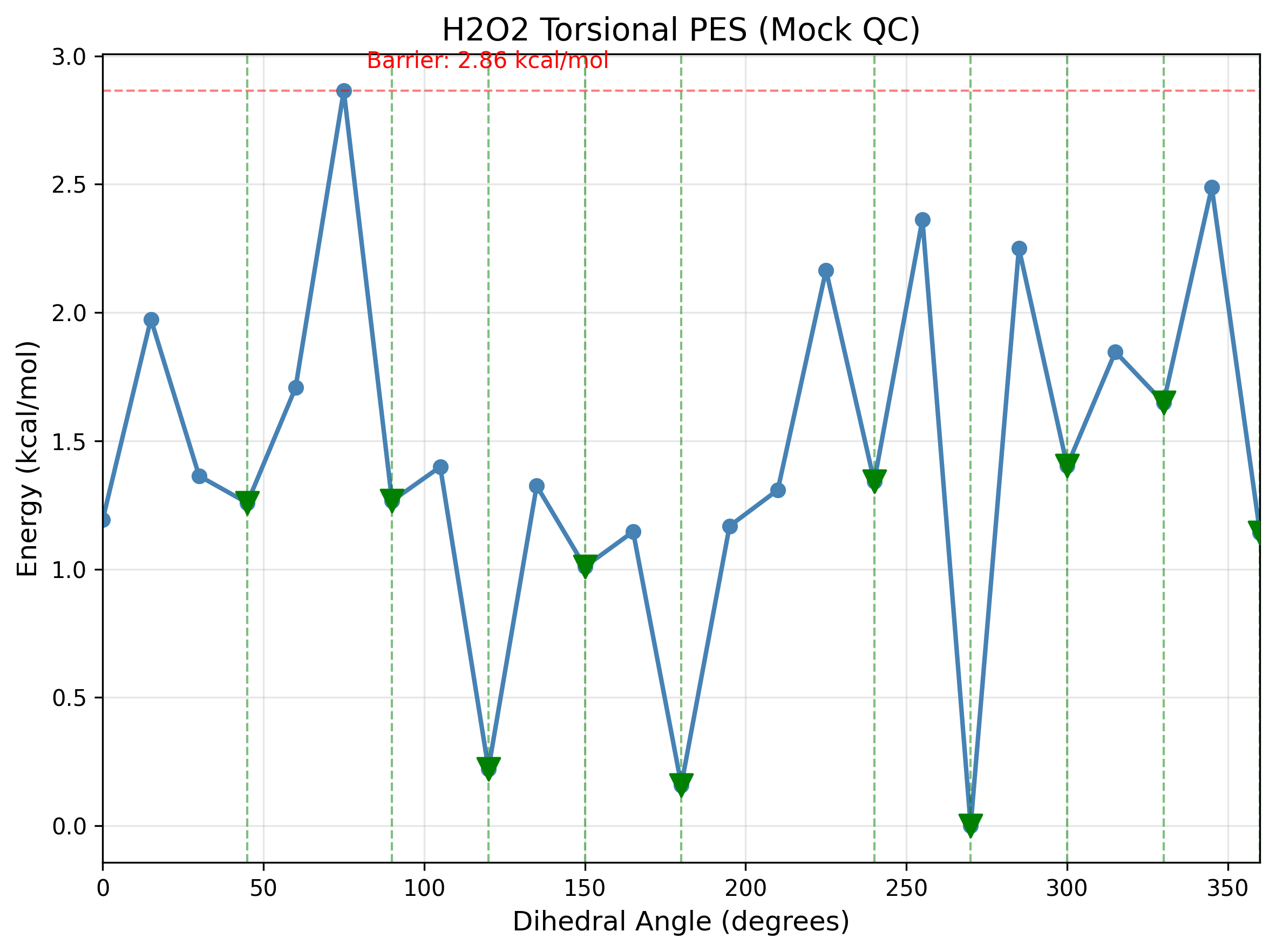
A relaxed scan was performed from 0 to 360 deg using a constrained dihedral. The mock engine provides a smooth, symmetric torsional barrier that is sufficient for workflow validation.
Tunneling corrections and energy grid
We evaluate a transmission function P(E) on a fractional grid of the barrier height and compute the tunneling correction kappa(T) as
\[ \kappa(T) = \frac{1}{k_B T} \int_0^{E_{max}} P(E) \exp\left(-(E - V_b)/(k_B T)\right)\, dE + \exp\left(-(E_{max} - V_b)/(k_B T)\right) \]
where V_b is the barrier height and the exponential tail accounts for energies beyond the computed grid. The grid uses 200 points, min_energy_ratio = 0.01, and max_energy_ratio = 1.05. The formula allows kappa < 1 when above-barrier reflection reduces transmission.
Instanton input (i-PI)
The workflow generates an i-PI XML input for a ring-polymer instanton calculation. The XML references an external driver that provides forces and energies.
Example configuration
from improved_tunnel.core.config import WorkflowConfig, TunnelingConfig, PESScanConfig, KineticsConfig
from improved_tunnel.workflow.runner import TunnelingWorkflow
from improved_tunnel.molecule.structure import Molecule
config = WorkflowConfig(
pes_scan=PESScanConfig(scan_type="relaxed", step_size=10.0),
tunneling=TunnelingConfig(methods=["WKB", "SCT", "Eckart"]),
kinetics=KineticsConfig(temp_min=100.0, temp_max=500.0, temp_step=20.0),
calculate_zpe=True,
)
workflow = TunnelingWorkflow(config, use_mock_engine=True)
state = workflow.run(Molecule.h2o2())i-PI input generation
from improved_tunnel.instanton import generate_instanton_input, IPIConfig
from improved_tunnel.molecule.structure import Molecule
mol = Molecule.h2o2()
config = IPIConfig(n_beads=32, temperature=300.0)
generate_instanton_input(mol, config=config, output_file="ipi_h2o2.xml")Table 1: Workflow settings
| Setting | Value |
|---|---|
| System | H2O2 torsion, H-O-O-H dihedral |
| PES scan | Relaxed, 0-360 deg, 10 deg step |
| Tunneling methods | WKB, SCT, Eckart |
| Energy grid | 200 points, 0.01-1.05 Vb |
| Temperature grid | 100-500 K, 20 K step |
| Prefactor | 1.0e13 s^-1 |
| QC engine | Mock (illustrative) |
Results and Discussion
The relaxed scan yields a symmetric torsional barrier of approximately 2.87 kcal/mol (mock value). The barrier height sets the scale for the transmission grid and for Arrhenius rate calculations.
Transmission coefficients rise sharply near the barrier. In this mock dataset, WKB and SCT track closely, while the analytic Eckart transmission turns on more abruptly above the barrier.[1,2]
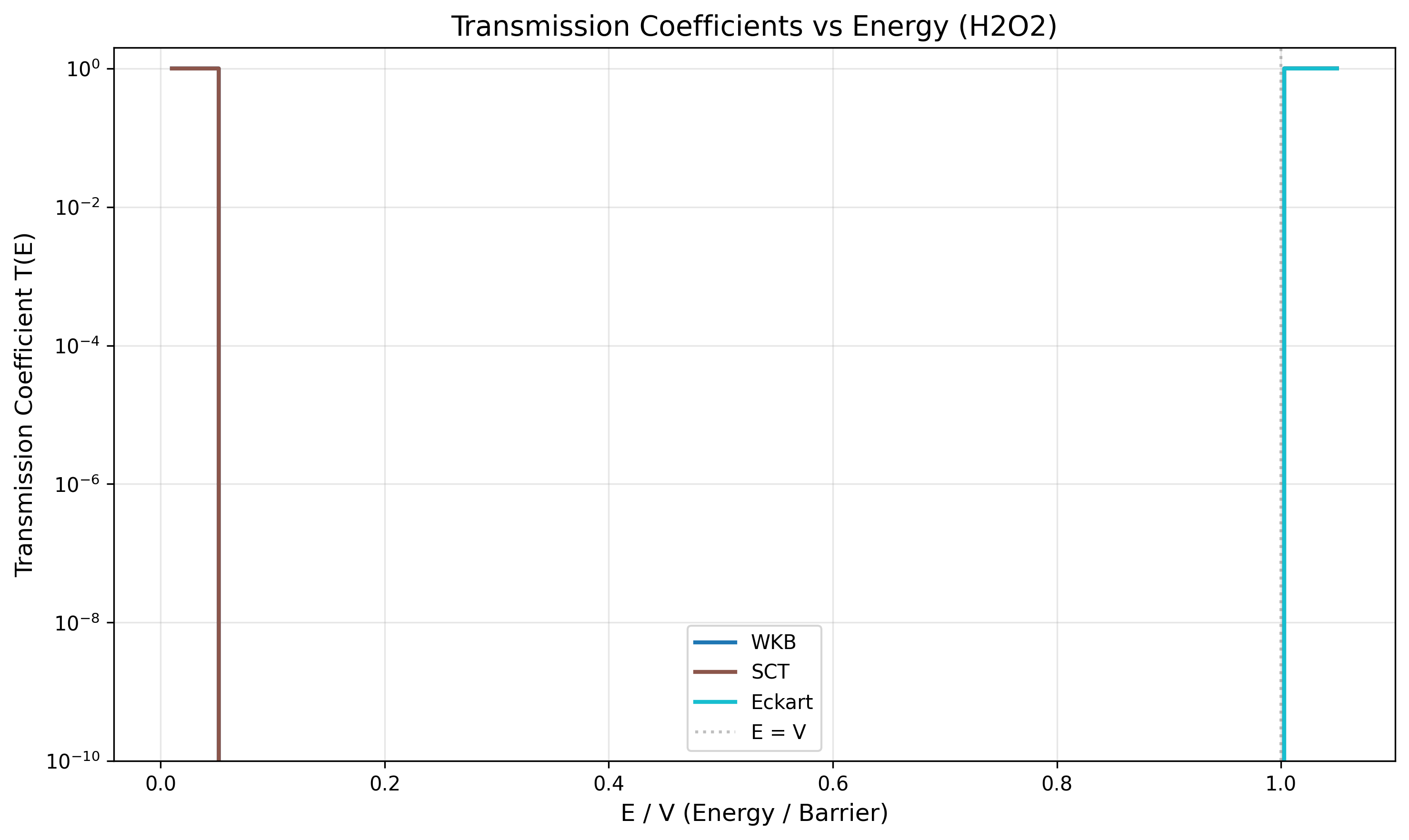
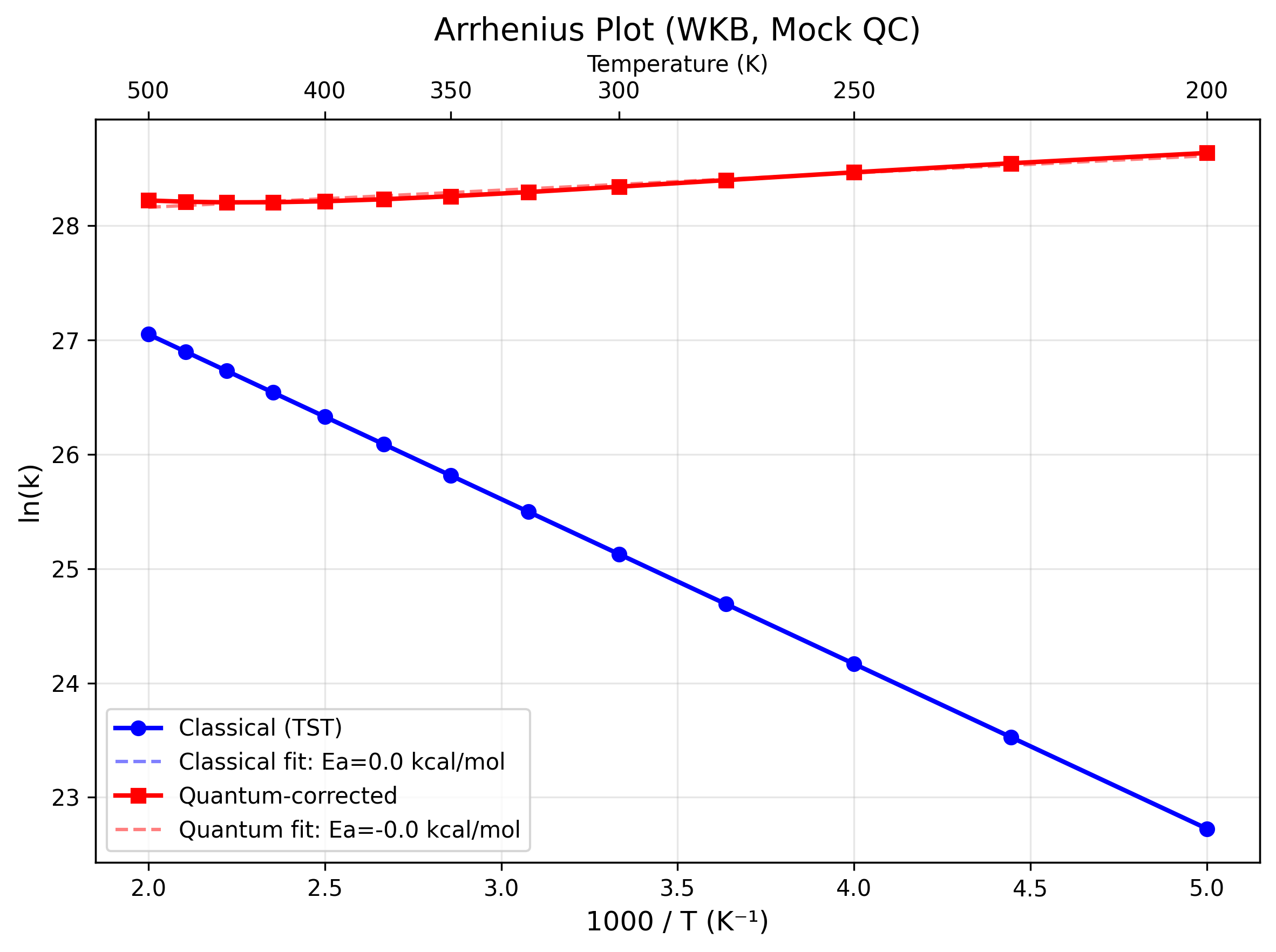
Table 2 summarizes kappa and rate constants at 300 K. The semiclassical methods yield strong tunneling enhancement (kappa >> 1), whereas the Eckart model is near the classical limit in this configuration. These values are illustrative and depend on the mock PES.
Table 2. Rate constants and tunneling corrections at 300 K (mock data).
| Method | kappa(300 K) | k_classical (s^-1) | k_quantum (s^-1) |
|---|---|---|---|
| WKB | 24.85 | 8.19e10 | 2.04e12 |
| SCT | 24.85 | 8.19e10 | 2.04e12 |
| Eckart | 1.01 | 8.19e10 | 8.25e10 |
The Arrhenius plot highlights the temperature dependence of kappa and the divergence between classical and quantum rates at low temperature.
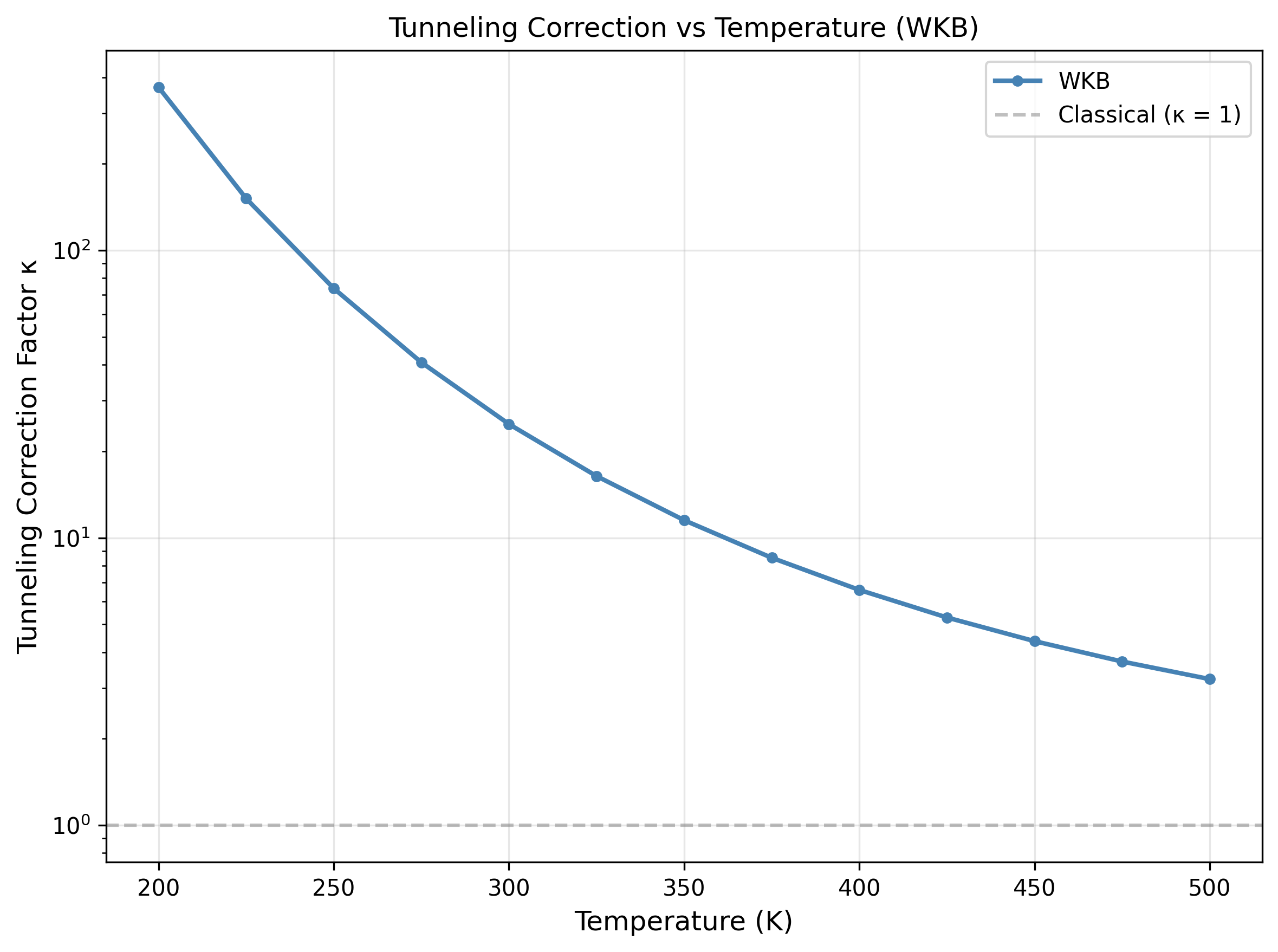
The kappa curve is monotonic with temperature and remains sensitive to the depth of the energy grid; using max_energy_ratio < 1 would underestimate kappa by omitting the above-barrier region.
Finally, the i-PI input enables an instanton optimization that can refine the deep-tunneling rate. The schematic below shows a 32-bead ring polymer representing the instanton path at 300 K.[3,4]

Practical Usage
To reproduce the workflow and print rate constants:
python -m pip install -e .
python examples/h2o2_tunneling.pyUse --real to call Psi4 instead of the mock engine:
python examples/h2o2_tunneling.py --realThe workflow returns structured dictionaries (angles, energies, transmissions, kappa values) that can be plotted with matplotlib. A minimal PES plot is shown below:
import numpy as np
import matplotlib.pyplot as plt
from improved_tunnel.core.constants import HARTREE_TO_KCAL
angles = np.array(state.pes_result["angles"])
energies = np.array(state.pes_result["energies"])
rel_kcal = (energies - energies.min()) * HARTREE_TO_KCAL
plt.plot(angles, rel_kcal)
plt.xlabel("Dihedral angle (deg)")
plt.ylabel("Relative energy (kcal/mol)")
plt.tight_layout()
plt.show()Limitations and Future Work
The mock engine does not reproduce ab initio energetics, so all numbers shown here should be treated as workflow demonstrations. For publishable results, the scan should be recomputed with Psi4 or ORCA and the instanton optimization should be converged with an external driver. A natural next step is to compare semiclassical kappa(T) against a full ring-polymer instanton rate for the same PES.
Authorship and Provenance
This post, the computational setup, and all figures were generated by an AI system using the improved_tunnel repository. The intent is transparency and reproducible workflow documentation rather than reporting new experimental measurements.
References
- Eckart, C. The Penetration of a Potential Barrier by Electrons. Phys. Rev. 1930, 35, 1303-1309. DOI: 10.1103/PhysRev.35.1303.
- Kastner, J. Theory and Simulation of Atom Tunneling in Chemical Reactions. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 158-168. DOI: 10.1002/wcms.1156.
- Richardson, J. O.; Althorpe, S. C. Ring-Polymer Instanton Method for Calculating Tunneling Splittings. J. Chem. Phys. 2009, 131, 214106. DOI: 10.1063/1.3267315.
- Ceriotti, M.; Cuny, J.; Parrinello, M.; Manolopoulos, D. E. i-PI: A Python Interface for Ab Initio Path Integral Molecular Dynamics Simulations. Comput. Phys. Commun. 2014, 185, 1019-1026. DOI: 10.1016/j.cpc.2013.10.027.