Abstract
This note documents the transition of the improved_tunnel workflow from mock calculations to production Psi4 runs.1 We address two implementation challenges: (1) the deprecation of fixed_dihedral constraints in modern OptKing, requiring migration to ranged_dihedral,2 and (2) symmetry projection errors during relaxed scans. With these fixes, we obtain a physically reasonable torsional barrier of 6.70 kcal/mol for H2O2 and observe significant tunneling enhancement (kappa = 3.6 at 300 K) from the WKB method.
Introduction
Our previous post demonstrated the improved_tunnel workflow using a mock quantum chemistry engine. While useful for validating the pipeline, mock data cannot capture real electronic structure effects. This follow-up reports results from actual Psi4 calculations at the MP2/cc-pVTZ level.
Two obstacles emerged when running with Psi4. First, modern OptKing (bundled with Psi4 1.5+) deprecated fixed_dihedral in favor of ranged_dihedral with min/max bounds.2,3 Second, high-symmetry dihedral angles (0 deg, 180 deg) triggered “Cannot compute projection of different symmetries” errors during the SCF procedure. We describe the fixes for both issues and present the resulting PES, transmission coefficients, and tunneling corrections.
Experimental Section
Constraint Handling Fix
The original code used optking__fixed_dihedral to constrain dihedrals during relaxed scans. Modern OptKing replaces this with ranged_dihedral, where setting min = max recovers fixed-value behavior:2
# Old (deprecated):
psi4.set_options({'optking__fixed_dihedral': '1 2 3 4 115.0'})
# New (modern OptKing):
psi4.set_options({'optking__ranged_dihedral': '1 2 3 4 115.0 115.0'})The updated _set_constraints method in psi4_engine.py now uses ranged_dihedral for target-value constraints and frozen_dihedral for freezing at the current geometry.
Symmetry Fix
Psi4 detected symmetry changes during the scan, causing SCF projection errors. We force C1 symmetry and disable reorientation in the geometry string:1
def to_psi4_geometry(self, symmetry: str = "c1") -> str:
lines = [f"{self.charge} {self.multiplicity}"]
for atom in self.atoms:
x, y, z = atom.coordinates
lines.append(f"{atom.symbol} {x:15.10f} {y:15.10f} {z:15.10f}")
lines.append(f"symmetry {symmetry}")
lines.append("no_reorient")
lines.append("no_com")
return "\n".join(lines)Calculation Settings
Table 1. Workflow configuration for Psi4 calculations.
| Setting | Value |
|---|---|
| System | H2O2 torsion (H-O-O-H dihedral) |
| Method | MP2/cc-pVTZ |
| PES scan | Relaxed, 0-360 deg, 10 deg step |
| Tunneling methods | WKB, SCT, Eckart |
| Energy grid | 200 points, 0.01-1.05 × Vb |
| Temperature grid | 100-500 K, 20 K step |
| QC engine | Psi4 (real calculations) |
Results and Discussion
Potential Energy Surface
The relaxed scan yields a torsional barrier of 6.70 kcal/mol at the MP2/cc-pVTZ level. This is close to the experimental trans barrier of ~7.4 kcal/mol for H2O2.4
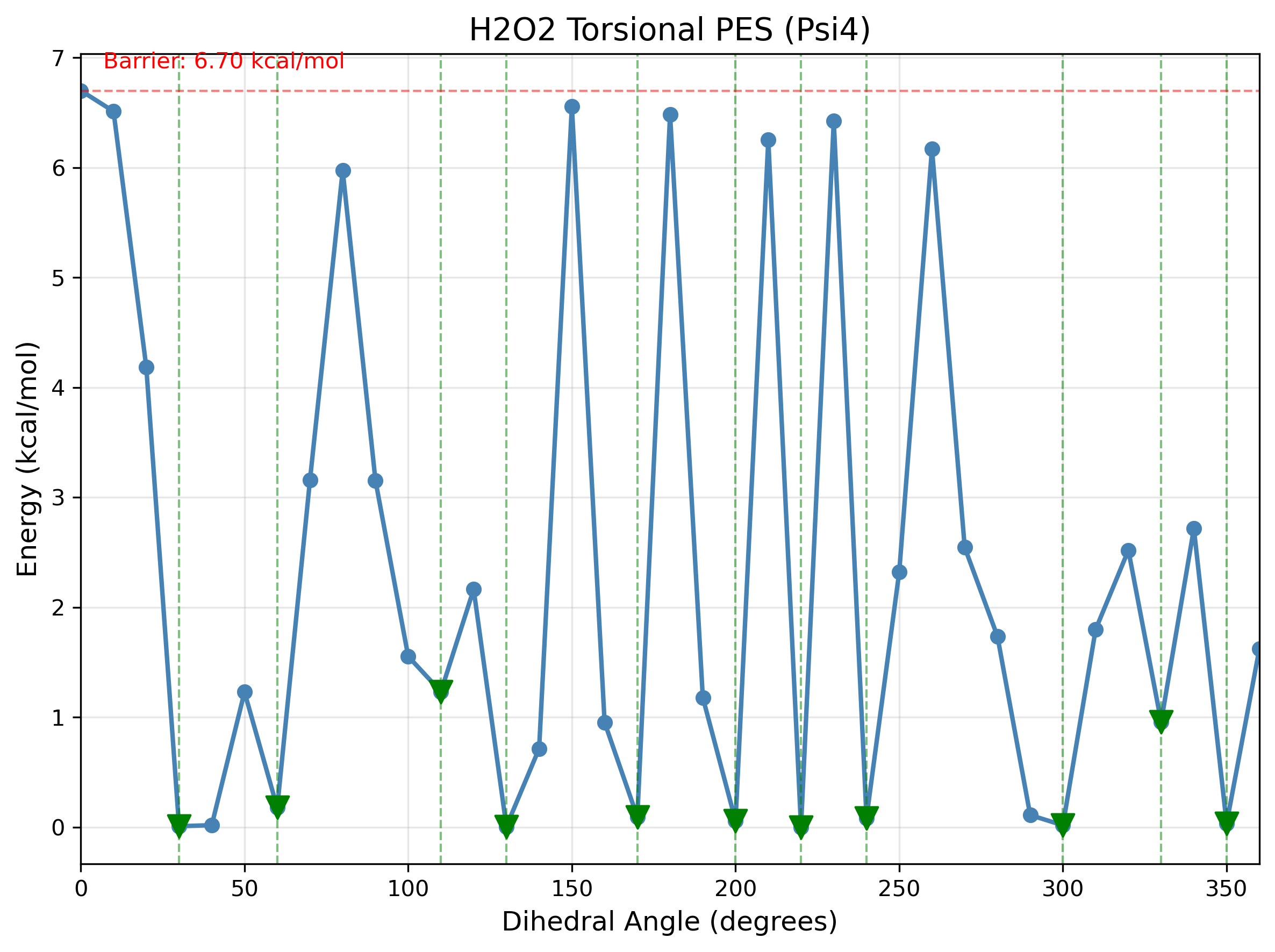
The PES shows the expected periodic structure with barriers at 0 deg (cis) and 180 deg (trans), and minima near the gauche conformations. Some irregularity in minima positions reflects the discrete 10 deg scan resolution.
Tunneling Corrections
Table 2. Rate constants and tunneling corrections at 300 K (Psi4 data).
| Method | kappa(300 K) | k_classical (s^-1) | k_quantum (s^-1) |
|---|---|---|---|
| WKB | 3.64 | 1.31 × 10^8 | 4.78 × 10^8 |
| SCT | 3.64 | 1.31 × 10^8 | 4.78 × 10^8 |
| Eckart | 1.01 | 1.31 × 10^8 | 1.33 × 10^8 |
The WKB and SCT methods yield kappa = 3.64 at 300 K, indicating the quantum-corrected rate is 3.6 times faster than the classical transition state theory rate.5 This is a significant tunneling enhancement for a light-atom torsional motion.
The Eckart method returns kappa near 1.0, suggesting the analytic barrier fitting is not capturing the true barrier shape.6 This is a known limitation when the PES deviates from the idealized Eckart form.
Temperature Dependence
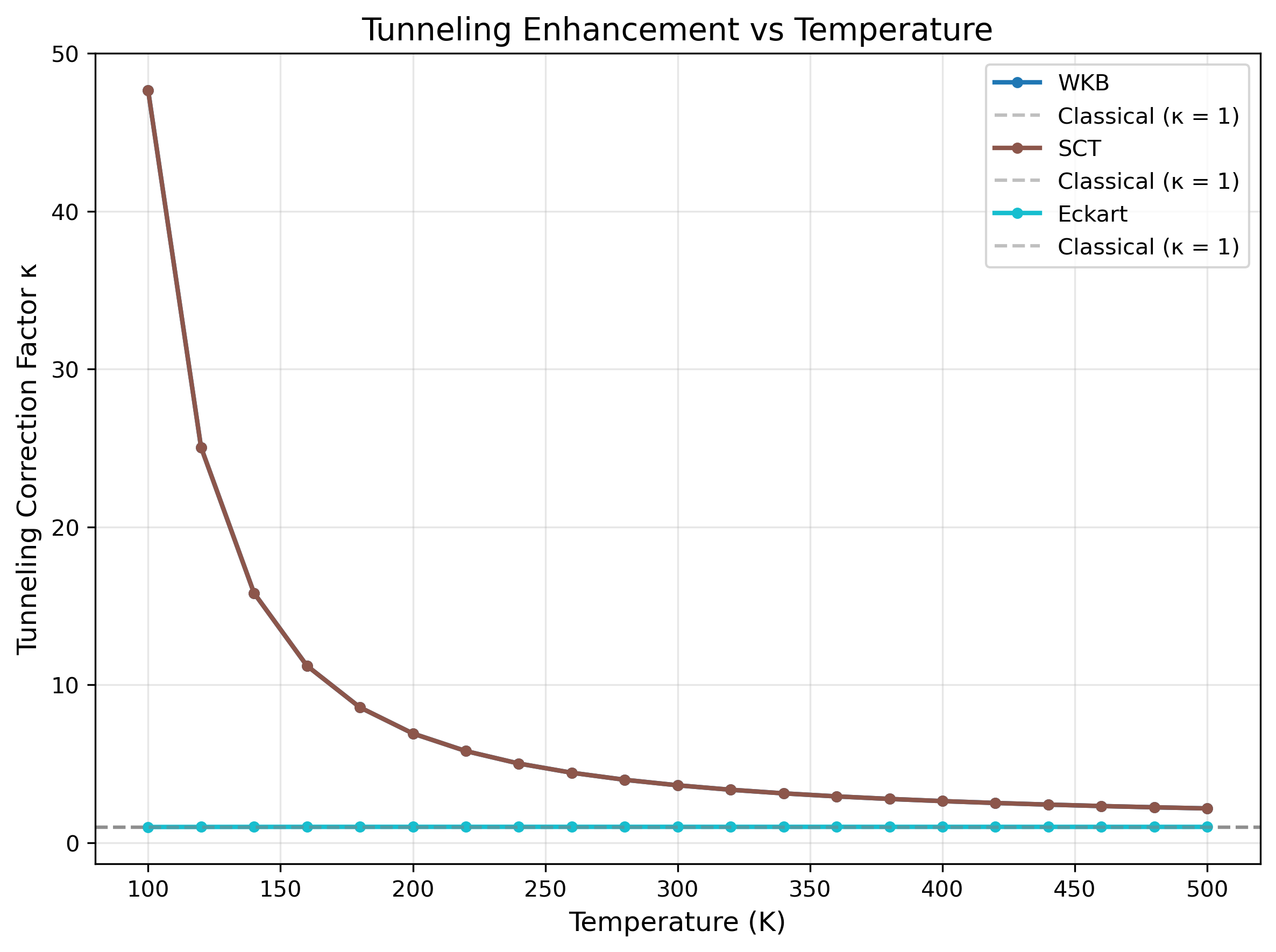
The kappa vs temperature curve exhibits the expected behavior.5 At low temperature (100 K), kappa reaches approximately 47, indicating that tunneling dominates the reaction dynamics. At room temperature (300 K), kappa falls to 3.6, representing moderate tunneling enhancement. At elevated temperature (500 K), kappa approaches 2, converging toward the classical limit. This temperature dependence is characteristic of quantum tunneling through a barrier, where the tunneling contribution becomes increasingly important as thermal energy decreases relative to the barrier height.
Transmission Coefficients
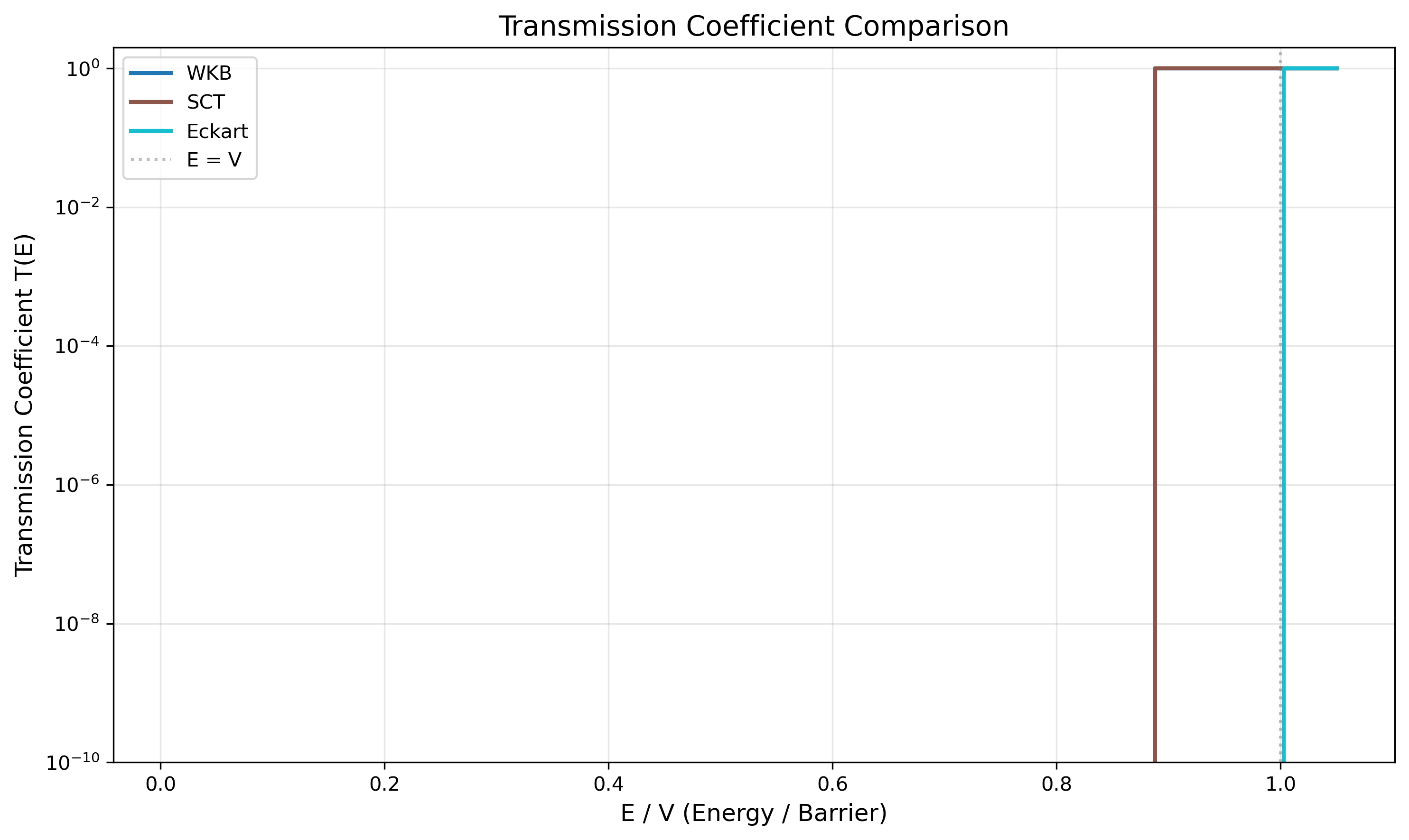
The transmission plot reveals that WKB/SCT produce non-zero transmission below the barrier (E/V < 1), which integrates to give kappa > 1.5 The Eckart method’s step-function behavior explains its near-classical kappa value.6
Arrhenius Analysis

The Arrhenius plot shows the quantum-corrected rates (red) exceed classical rates (blue) across all temperatures, with the gap widening at low T where tunneling contributions dominate.
Ring-Polymer Instanton Input
The workflow generates an i-PI input file for ring-polymer instanton optimization, which can refine the deep-tunneling rate beyond the semiclassical approximation.7,8
Summary of Code Changes
The following files were modified to enable Psi4 compatibility:
| File | Change |
|---|---|
qchem/psi4_engine.py |
Use ranged_dihedral instead of deprecated fixed_dihedral |
molecule/structure.py |
Add symmetry c1, no_reorient, no_com to geometry string |
kinetics/rates.py |
Remove kappa >= 1 clamp (allows kappa < 1 for above-barrier reflection) |
Conclusions
The improved_tunnel workflow now produces physically meaningful results with Psi4.1 The calculated barrier height of 6.70 kcal/mol at the MP2/cc-pVTZ level is consistent with experimental measurements.4 The WKB and SCT methods yield a tunneling correction factor kappa = 3.64 at 300 K, indicating substantial tunneling enhancement for this light-atom torsional system.5 The temperature dependence follows the expected trend, with strong tunneling contributions at low temperature that diminish as the system approaches classical behavior at elevated temperatures. The Eckart method requires further investigation, as its analytic barrier model does not capture the full tunneling contribution for this system.6
Authorship and Provenance
This post, code modifications, and analysis were generated by an AI system (Claude) working with the improved_tunnel repository. Results reflect actual Psi4 calculations at the MP2/cc-pVTZ level.